Sample Undergraduate Research Projects

Here is a list of recent undergraduate research projects. When available, we have added images that give you a flavor of some of the topics studied. If the student wrote a thesis, you can look it up at USM's library.

• Samuel Dent, "Applications of the Sierpiński Triangle to Musical Composition", Honors Thesis 
• Brandon Hollingsworth, "A time integration method for nonlinear ordinary differential equations", undergraduate research thesis.
• Haley Dozier, "Ideal Nim", undergraduate research project.
• Sean Patterson, "Generalizing the Relation between the 2-Domination and Annihilation Number of a Graph", Honors Thesis.
• Elyse Garon, "Modeling the Diffusion of Heat Energy within Composites of Homogeneous Materials Using the Uncertainty Principle", Honors Thesis.
• Brandi Moore, "Magic Surfaces", Mathematics Undergraduate Thesis.
• Amber Robertson, "Chebyshev Polynomial Approximation to Solutions of Ordinary Differential Equations", Mathematics Undergraduate Thesis
• Kinsey Ann Zarske, "Surfaces of Revolution with Constant Mean Curvature H=c in Hyperbolic 3-Space H³(-c²)", Undergraduate Student Paper Competition, 2013 meeting of the LA/MS Section of the MAA.

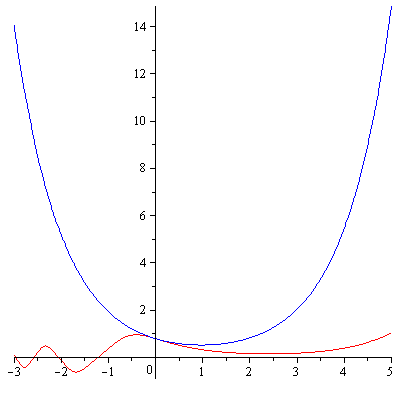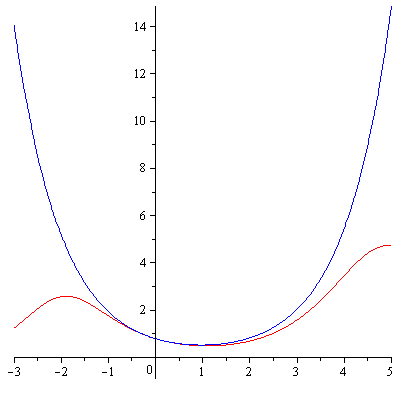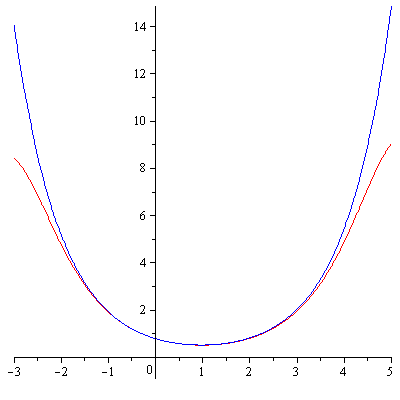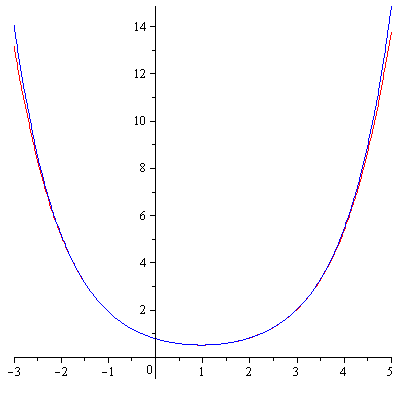
• Lorrin Debenport, "Row Reduction of Macauley Matrices", Honors Thesis, 2011.
  

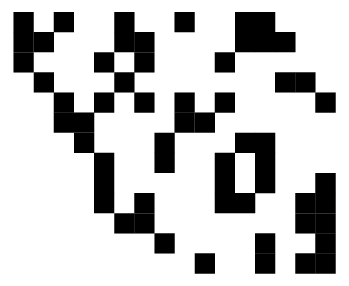
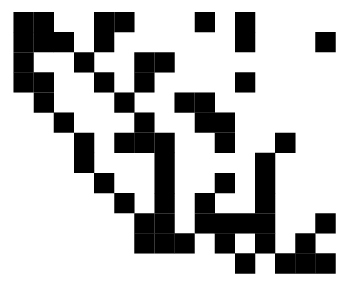
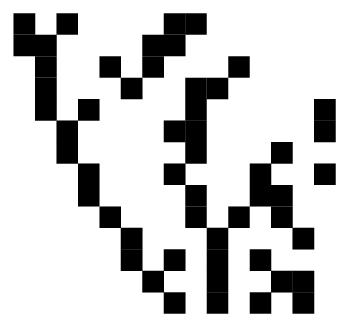
  Examples of the near-triangularity of the Macaulay matrix.

• Benjamin Benson, "Special Matrices, the Centrosymmetric Matrices", Undergraduate Thesis, 2010.
• Matthew Dixon, "Tropical Mathematics", Undergraduate Project, 2010.
  

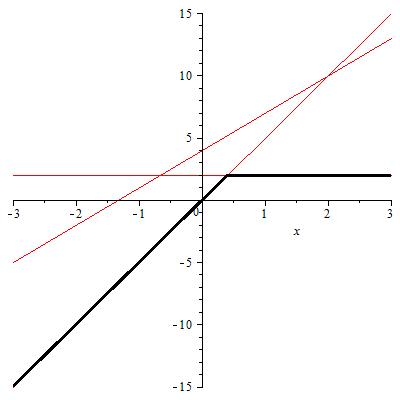
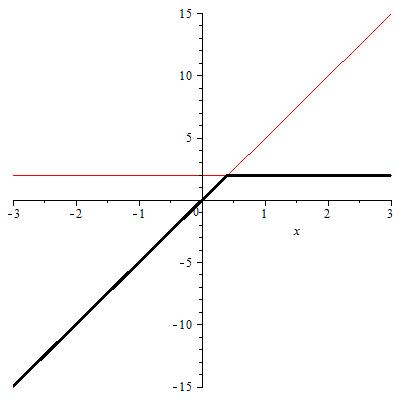
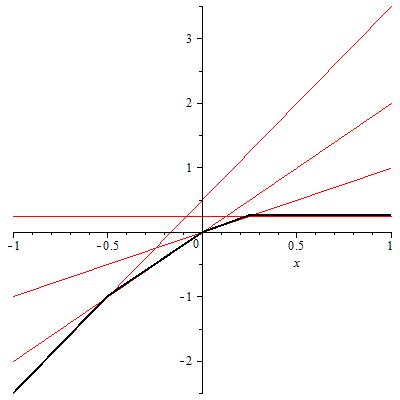
  One line contributes nothing to the tropical polynomial on the left. The tropical polynomial on the right is fully reduced, because all the lines contribute.		A dense tropical polynomial: if the slope of line i is mi, then mi+1 = mi+1.

• Elisabeth Palchak, "A criterion for identifying stressors in non-linear equations using  Gröbner bases", Honors Thesis, 2010.
  

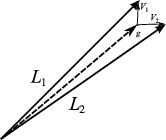
  Trying to compute a vector common to L1 and L2 gives rise to an interesting multivariate, polynomial system.

• Christopher R. Mills, "Method of approximate fundamental solutions for ill-posed elliptic boundary value problems", Honors Thesis, 2009.
• Ashley Sanders, "Problems in the College Math Journal", Undergraduate Project, 2009.
• Deanna Leggett, "Dodgson's method of computing determinants", Undergraduate Project, 2008.
  
  

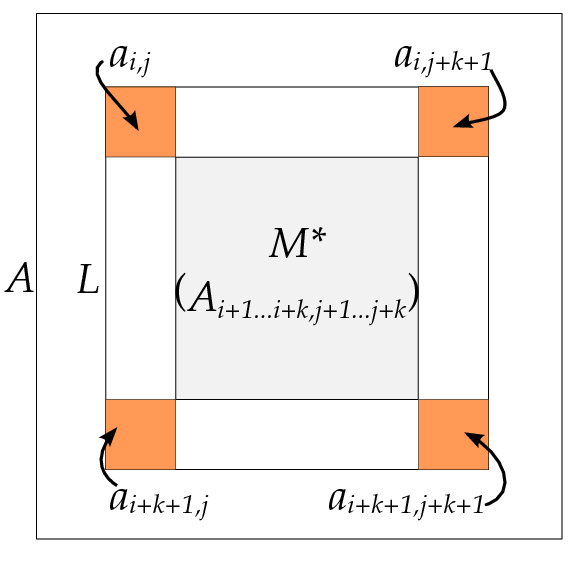
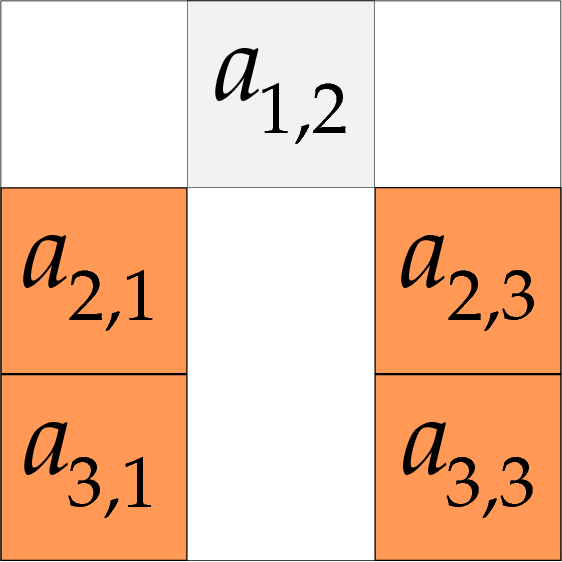
  Dodgson's Method fails if an interior matrix has determinant zero.	The double-crossing method fixes this by choosing a different matrix for the division. More details in the full paper.